Alexandr A.Shpilman ( alexandrshpilman78@gmail.com )
Playing with photon
|
Abstract: There will be no infinite fall of a photon
into a "black hole". (There will be no infinite fall for other
elementary particles either.) The actual size of a photon is significantly
smaller than expected. |
Photon
energy:
|
|
W = h* v = 2q0*Ô0*v = 2q0*Ô0*c0 /λ |
(1) |
Where:
|
|
h - |
planck constant, |
|
|
v - |
frequency, |
|
|
q0 - |
electron charge, |
|
|
Ô0 - |
magnetic flux quantum, |
|
|
c0 - |
speed of light, |
|
|
λ - |
wavelength. |
Three
"constants" in one formula and the last expression resembles electric
potential:
|
U = q/(ε*R) |
(2) |
Ãäå:
|
ε - |
permittivity, |
|
|
|
q - |
electric charge. |
From formula (1):
|
|
W = 2q0*Ô0*c0 /λ = q0* U |
(3) |
For a
photon we have:
|
|
U = 2*Ô0*c0 /λ |
(4) |
Gravitational potential:
|
|
F = g*M/R |
(5) |
Where:
|
|
g - |
gravitational constant, |
|
|
M - |
mass of an object. |
The speed
of time, the speed of light, the refractive index n (of light) change in
a gravitational field:
|
|
n = n0*exp(2*F/c2) = n0*(1+1*10-10 ) |
(6) |
This small
change in the refractive index of a vacuum causes gravity. (More details in the
article "Gravitational Field")
At large
gradients of the refractive index n, the light flow will be reflected.
For this to happen, there must be:
|
|
(d n/ d R) * (λ/4n) ≥ 1 |
(7) |
Either
|
|
(2*F/c2) *( λ/4) ≥ R |
(8) |
Given that
|
|
R = sqrt((2* g*M /c2) * (λ/4)) |
(9) |
Where
sqrt - square root function.
The
emergence of a resonant electromagnetic standing wave is possible. For example,
let's take a photon of the visible spectrum with a wavelength of 5*10-7
m. For the gravitational field of the Earth, we get R=3.3*10-5
m. This is less than the gravitational radius of a black hole with the mass of
the Earth (Rg = 9*10-3 m). R=2*10-2
m in a black hole with the mass of the Sun (Rg=3*103
m)
That is, there will be no infinite fall of a photon into a "black
hole". (There will be no infinite fall for other elementary
particles either.)
It is
possible to assume that the past, present and future continuously exist in a
five-dimensional space-time. Our perception of time, our "now" is
tied to a gravitational wave that spreads in a five-dimensional space-time
(there is a justification for such an assumption, more details "Time - Overtime (N2/00)"), so that we
perceive only a four-dimensional space-time.
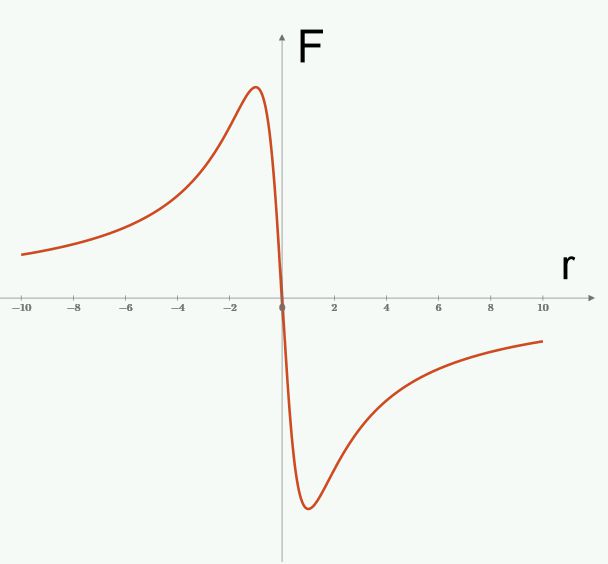
Fig. 1
shows a variant of the graph of the change in the gravitational potential in a
gravitational wave ("soliton"). Fig. 2 shows a graph of the
corresponding change in the refractive index of the vacuum in a gravitational
wave.
|
|
|
|
Fig.1 |
Fig.2 |
Let's
assume that one radiation flux Io
comes from the right side, is reflected and returns back. Part of this flux
crosses the gravitational wave (going into the negative part of the graph along
the r axis).
|
|
Ip = I1 *(1 + ((ns -1)/( ns +1))2 ) |
(10) |
Where:
I1 – some initial radiation flux,
ns – the ratio of the refractive index of the
physical vacuum in the region r=0 between the values of ns on the right and left sides of the
graph.
Let's
assume that a second radiation flux I2
comes from the left side, is reflected and returns back. Part of this flux Ie
intersects the gravitational wave (going to the positive part of the graph
along the r axis).
|
|
Ie = I2 *(1 – ((ns -1)/( ns +1))2 ) |
(11) |
Let's
assume that our "now" is in the interval between the numbers 1 and 2
on the r axis. Let's assume that all the energy of the proton is
concentrated in this "now". And the electron is the flow Ie that
the gravitational barrier has penetrated from the left. In this version,
|
|
Ip/Ie ~ mp/me ~ ns ~ 1833 |
(12) |
(More
details in "Time - Overtime (N1/13)")
For a
proton in our current n = ns/2.
Let's
assume that the main mass/energy of the proton is tied to the very bottom of
the gravitational well. Let's take equations (6) as a basis. The condition of a
resonant standing wave (half-wave):
|
|
(d n/ d R) * (λp/2n) = 1 |
(13) |
Assuming
that at the “bottom” R= λp/2 and n
≈ 900, from formula (6):
|
|
np = n0*exp(Fp/R) = n0*900 |
(14) |
We find: Fp ≈ 4.5*10-15 m. Then for the
electron position:
|
|
(d n/ d R) * (λe/4n)
= 1 R = sqrt(Fp * λe/4
) ≈ 5.2*10-14 ì. ne ≈ 1.09 |
(15) |
For a visible
spectrum photon with a wavelength of 5*10-7 m. We will receive a
reflection from the "depth" of the gravitational well at a distance
of R≈2.4*10-11 m, with nf
≈1.00019. It turns out that the energy of a photon with a wavelength of
5*10-7 m is mainly concentrated in a significantly smaller volume. It becomes clearer how a photon is emitted and absorbed as a
whole when interacting with an electron. (This is probably why a
ferromagnetic antenna based on a ferrite rod is effective in radio receivers.)
Thus, the
movement of a photon (proton, electron, etc.) in our “now” should be considered
as movement in a thin film with n≠1. (In a two-dimensional
version, the analogue is optical fiber.)
It is worth
considering that all these length values - are
determined from the side of an external observer
where n=1.
The
nonlinearity of the vacuum can manifest itself not only in a change in the
refractive index, but also in a change in the wave resistance of the vacuum.
Thus, the value of the latter differs for a photon (ρf)
and an electron (ρe):
|
|
ρe/ρf ≈137/2 |
(16) |
(more
details in "Interesting Relationships")
Similar to
formula (13), the condition for a resonant standing wave (quarter-wave):
|
|
(d ρ/ d R) * (λp/4ρ) = 1 |
(17) |
***
Of course,
these constructions are only new inputs for determining the nature of
the photon.