Alexander A.Shpilman ( alexandrshpilman78@gmail.com )

Russian

Time - Overtime

(Continuation, the beginning see in N2/00 )

Fig.1

Let us assume that the electron is a fragment of the radiation flux from the past to the future manifested in our gap now.

Suppose that the proton is a fragment of the radiation flux from the future into the past manifested in our gap now.

"Our gap now" is a certain three-dimensional gravitational wave propagating along the axis of "our time" T in the overtime O.

Let us assume that the difference in the mass of an electron and a proton is due to the relativistic Doppler effect. In this case, approximately:

mp/me = γ^2 = 1/(1-(Vt/Co)^2)

(1)

Here:

m_p - is the proton mass,

m_e - s the mass of an electron,

V_t - is the speed of the time wave in the OVERTIME,

C_o - is the speed of light in the OVERTIME.

Let us assume that V_t is equal to our speed of light C (in our "gap now"). Then from formula (1) we have:

Co = C / SQRT(1-me/mp) = 2.999* 10^8 m/s

(2)

It turns out that C_o is greater than C by only 0.027%. Those, the speeds are almost equal.

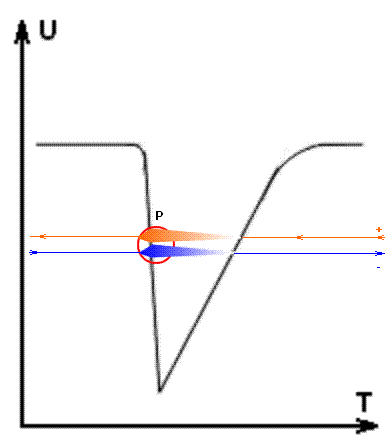
Let us assume that C is less than C_o due to an increase in the refractive index of the physical vacuum. In this version, we will try to determine what difference in the refractive indices can give the difference in the masses of the electron and proton due to reflection at the medium interface. Suppose that the leading edge of the "now" wave is blurred as shown by the black line in the graph in Fig.1. And the rear front represents a sharp boundary between the "medium partition". Then the next fraction of the radiation (relativistic effects are not taken into account yet) will pass into our "now" through the boundary for the electron:

Ie = Io *(1 – ((n-1)/(n+1))^2 )

(3)

Here:

I_o - is some initial radiation flux,

n - is the ratio of the refractive index of the physical vacuum in our gap "now", with respect to the refractive index of the physical vacuum in the outside.

For the proton, in our gap "now", there will be an overlap of incoming radiation and reflected:

Ip = Io *(1 + ((n-1)/(n+1))^2 )

(4)

Let’s n is much greater than 1. Then:

I_e ~ I_o *(2/n)

I_p ~ I_o *2

I_p/I_e ~ m_p/m_e ~ n ~ 1833

It should be beyond our "now" gap, outside the "wave of time" of our "now" speed "light" C_o is more in 1833 times our speed of light C. If it so, it is very encouraging for interstellar travel. This is the "hyperspace" that fantasists like to dream about.

Naturally, the obtained figure is very approximate. It, for example, is not taken reflection of radiation between neighboring "time waves" into account and various nonlinear effects are not taken into account.

***

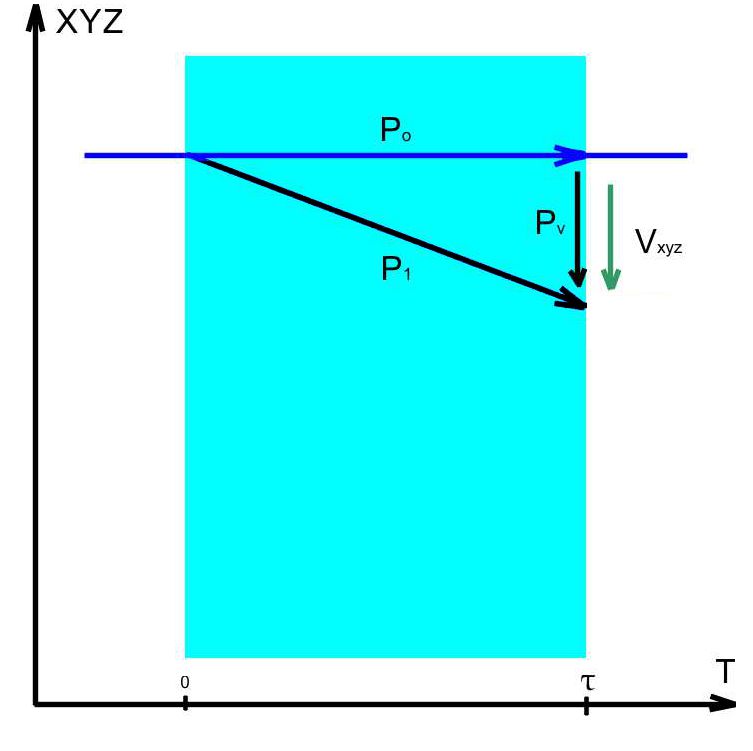
Fig.2

A change in the speed of the particle in the "now" along the XYZ coordinates will lead to a change in the slope of the global line (Fig.2). In this case, impulse of the particle becomes:

P1^2 = Po^2 + PV^2

(5)

Where:

P_o - is the initial momentum of the particle,

P_V - is transmitted by the particle impulse of the motion along the XYZ coordinates.

The speed C propagation of mass/energy along the global line remains unchanged. If we start from the law of conservation of momentum, it remains to assume that the mass of the particle changes. Then equation 5 is transformed into:

(m1 *C )^2 = (mo *C )^2 + (m1 *V )^2

(6)

Where:

V - is the speed of particle along the coordinates XYZ,

m_o - is the mass of "rest" particle,

m₁ - is the mass of particle with speed V.

If we solve equation 6, we get:

m1 = mo /SQRT(1 - (V/C)^2) = γ * mo

(7)

The relativistic change of the mass particle arise by itself.

Waves of de Broglie

We find in the handbook on physics the formula for determining the wavelength of de Broglie, the particle of mass m with the speed of motion V:

λ = h /( γ*m*V)

(8)

Where:

h - is the constant of Planck.

We should note that speed is the relative magnitude of the objects of interaction, and not absolute speed relative to the "Universe navel" (even if it is the experimenter himself). We will try to derive formula 8, based on our model. We assume that the frequency of the wave process in the "global line" of the particle is equal to:

fo = (mo*C^2)/(2*h)

(9)

Fig.3

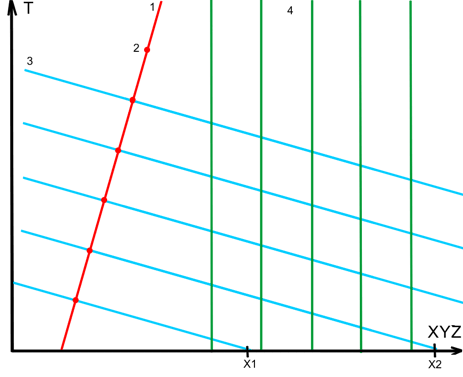
The numerator is divided into two because in the "global line" we have a straight and reflected wave in our gap "now". And it is unlikely that our gap "now" is similar to a moving glass. Most likely this wave is of change the physical properties of the vacuum. Accordingly, a straight and reflected wave forms a standing wave along the global line of particle 1 (the red line in Fig. 3) with nodes of antinode 2 (red dots on line 1) spaced at a distance:

lo = Co / (2*fo ) = h/ (mo*C)

(10)

The coordinate system in Fig.3 is tied to the crystal lattice. The global lines 4 (green) of its atoms are shown in this figure.

We show the convergence of our test particle with the crystal lattice by the slope of the global line 1 to the global lines 4.

The phase planes of a standing wave 3 in 1 cross the "now" line of the crystal at points X1, X2, ... The distance between these points is equal to:

Lo = X2 - X1 = lo /(V/C)= lo * Co / V = h/ (mo*V)

(11)

For the relativistic case:

λ = Lo / γ = h /( γ*mo*V)

(12)

Exactly, this is characteristic length of wave (the de Broglie wave). It will characterize the diffraction of the moving particle at the sites of the crystal lattice.

Thematic Contents

CONTENTS