Александр А.Шпильман ( alexandrshpilman78@gmail.com )

English

Время - Надвремя

Рис.1

(Продолжение, см. начало в N2/02)

Положим, что электрон это фрагмент потока излучения из прошлого в будущее проявленный в нашем зазоре сейчас.

Положим, что протон это фрагмент потока излучения из будущее в прошлое проявленный в нашем зазоре сейчас.

"Наш зазор сейчас" это некая трехмерная гравитационная волна распространяющаяся по оси "нашего времени" Т в надвремени О.

Положим что разница в массе электрона и протона обусловлена релятивистским эффектом Доплера. В таком варианте приблизительно:

mp/me = γ^2 = 1/(1-(Vt/Co)^2)

(1)

Где:

m_p – масса протона,

m_e – масса электрона

V_t – скорость волны времени в надвремени,

C_o – скорость света в надвремени.

Положим V_t равна нашей скорости света C (в нашем зазоре сейчас). Тогда из (1) имеем:

Co = C / SQRT(1-me/mp) = 2.999* 10^8 м/сек

(2)

Получается C_o больше C всего лишь на 0.027%. Т.е. скорости почти равны.

***

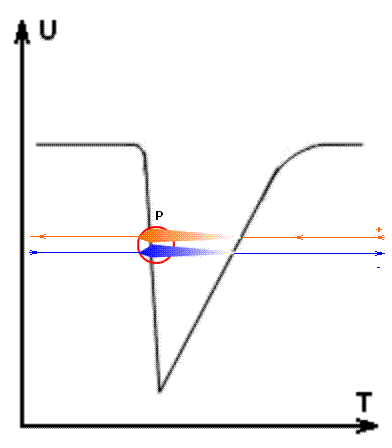
Положим то что C меньше C_o за счет увеличения показателя преломления физического вакуума. В этом варианте попробуем определить какая разница показателей преломления может дать разницу в массах электрона и протона за счет отражение на границе раздела сред. Положим, что передний фронт волны "сейчас" размыт как показано черной линией на графике на Рис.1. А задний фронт представляет резкую границу "раздела сред". Тогда для электрона сквозь границу пройдет в наше "сейчас" следующая доля излучения (релятивистские эффекты пока не учитываем):

Ie = Io *(1 – ((n-1)/(n+1))^2 )

(3)

Где:

I_o – некий изначальный поток излучения,

n – отношение показателя преломления физического вакуума в нашем зазоре "сейчас", по отношению к показателю преломления физического вакуума во вне.

Для протона, в нашем зазоре "сейчас", произойдет наложение приходящего излучения и отраженного:

Ip = Io *(1 + ((n-1)/(n+1))^2 )

(4)

Положим n много больше 1. Тогда:

I_e ~ I_o *(2/n)

I_p ~ I_o *2

I_p/I_e ~ m_p/m_e ~ n ~ 1833

Получается вне нашего зазора "сейчас", вне "волны времени" нашего "сейчас" скорость "света" C_o больше в 1833 раз нашей скорости света C. Если так, то это весьма обнадеживающе для межзвездных путешествий. Это то "гиперпространство" о котором любят мечтать фантасты.

Естественно, полученная цифра весьма приблизительная. Поскольку, например, не учтено отражение излучений между соседними "волнами времени" и не учтены разного рода нелинейные эффекты.

***

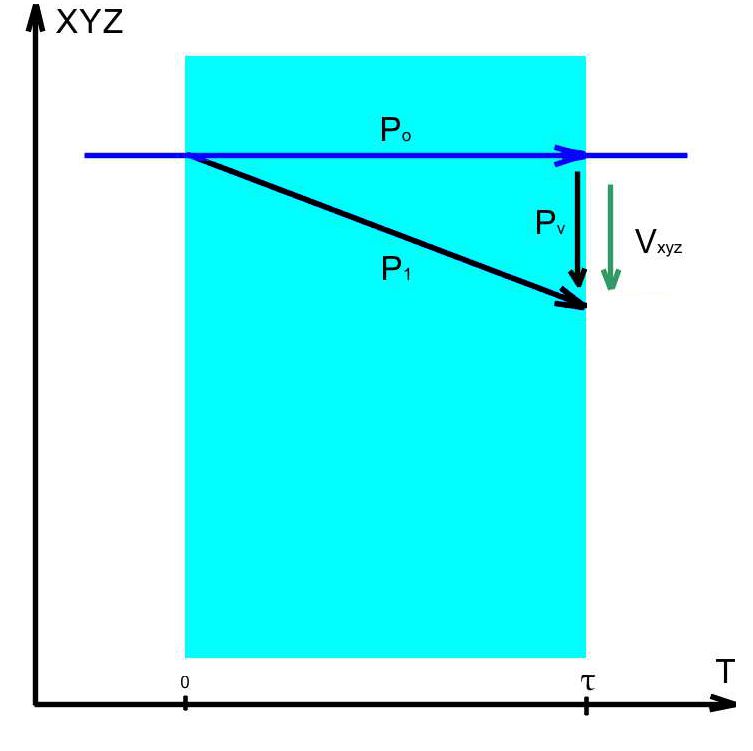
Рис.2

Изменение скорости частицы в "сейчас" вдоль координат XYZ приведет к изменению наклона глобальной линии (см. Рис.2). При этом импульс частицы станет равен:

P1^2 = Po^2 + PV^2

(5)

Где:

P_o – первоначальный импульс частицы,

P_V – переданный частице импульс движения вдоль координат XYZ .

Скорость C распространения массы/энергии вдоль глобальной линии остается неизменным, исходя из закона сохранения импульса остается предположить что изменяется масса частицы. Тогда уравнение 5 преобразуется в:

(m1 *C )^2 = (mo *C )^2 + (m1 *V )^2

(6)

Где:

V – скорость частицы вдоль координат XYZ,

m_o – масса "покоя" частицы,

m₁ – масса частицы со скорость V.

Решая уравнение 6 получим:

m1 = mo /SQRT(1 - (V/C)^2) = γ * mo

(7)

Релятивистское изменение массы частицы получилось само собой.

Волны де Бройля

Заглянув в справочник по физике мы найдем формулу для определения длины волны де Бройля частицы масс m со скоростью движения V:

λ = h /( γ*m*V)

(8)

Где

h - постоянная Планка.

Дополнительно стоит отметить что скорость является относительной объектов взаимодействия, а не абсолютная скорость относительно "Пупа Вселенной" (даже если это сам экспериментатор).

Попробуем вывести формулу 8 исходя из нашей модели, положив что частота волнового процесса в "глобальной линии" частицы равна:

fo = (mo*C^2)/(2*h)

(9)

Рис.3

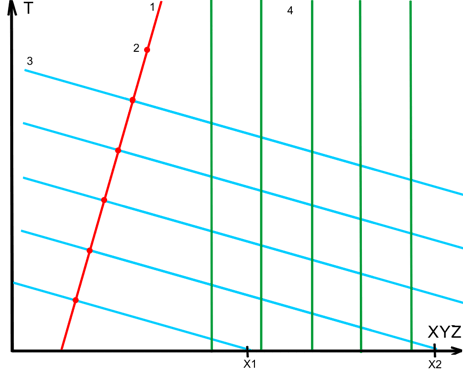
Числитель делится на двойку поскольку в "глобальной линии" имеем прямую и отраженную волну в нашем зазоре "сейчас". И маловероятно что наша зазор "сейчас" подобен движущемуся стеклу. Наиболее вероятно это волна изменения физических свойств вакуума. Соответственно прямая и отраженная волна образует стоячую волну вдоль глобальной линии частицы 1 (красная линия в Рис.3), с узлами пучности 2 (красные точки на линии 1), отстоящих на расстоянии:

lo = Co / (2*fo ) = h/ (mo*C)

(10)

Система координат на Рис.3 привязана к кристаллической решетке, глобальные линии 4 (зеленые) ее атомов показаны на этом рисунке.

Сближение нашей пробной частицы с кристаллической решеткой показано наклоном глобальной линии 1 к глобальным линиям 4.

Фазовые плоскости стоячей волны 3 в 1 пересекают линию "сейчас" кристалла в точках X₁,X₂,… , так что расстояние между этими точками равна:

Lo = X2 - X1 = lo /(V/C)= lo * Co / V = h/ (mo*V)

(11)

Для релятивистского случая:

λ = Lo / γ = h /( γ*mo*V)

(12)

Именно это характерная длина (волны де Бройля) и будет характеризовать дифракцию движущейся частицы на узлах кристаллической решетки.

Тематическое содержание

СОДЕРЖАНИЕ