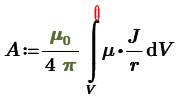Александр А.Шпильман ( alexandrshpilman78@gmail.com )

English

Физика и/или математика

 

Ныне настолько «физики» обожествили математику, что в статьях и учебниках потерялась сама физика. Для примера возьмем кое-что из квантовой «механики». Так изменение импульса электрона P(x) при движении в электромагнитных полях записывают так:

 

 

P(x)=P0-SQRT(q*U(x)*m)– q *A(x)/c

(1)

 

где

P0 – начальный импульс электрона;
U – электрический потенциал;
A – магнитный векторный потенциал;
q  - электрический заряд электрона;
m – масса электрона;
c – скорость света;
SQRT – квадратный корень.

 

Изменение относительной фазы волновой функции:

 

 

df~P(x)*dx= (P0-SQRT(q*U(x)*m)– q*A(x)/c)*dx

(2)

 

Если изменения импульса электрона в электрических полях очевидно, то причем здесь магнитный векторный потенциал A ?

Полагается что магнитная индукция:

 

 

B = rot A

(3)

 

И напряженность электрического поля:

 

 

E = - dA/dt

(4)

 

Какой смысл в такой придумке как магнитный векторный потенциал A ?

Для примера рассмотрим обычный электрический трансформатор на Рис.1

 

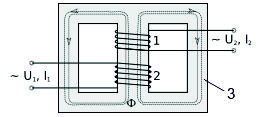
Рис.1

Где 1 и 2 - первичная и вторичные электрические обмотки. 3 – ферромагнитный сердечник трансформатора.

Все магнитное поле сосредоточено в ферромагнитном сердечнике трансформатора. Его влияние на электрические обмотки минимально. Основным фактором действующим электрические обмотки 1 и 2 является магнитный векторный потенциал A. И электрическое поле индукции определяется по формуле (4).

Прежде чем вернутся к формулам (1) и (2), рассмотрим Фото.1 и Фото.2, где 1 – электрический проводник, 2 – ферритовое кольцо, 3 – электрическая обмотка на ферритовом кольце.

 

Фото.1

Фото.2

 

Индуктивность электрических «катушек» на Фото.1 и Фото.2 равна:

 

 

L ≈ µ0*µ*N2/(l/S)

(5)

 

где

µ0 – магнитная проницаемость вакуума;
µ – магнитная проницаемость материала ферритового кольца;
N – количество витков в катушке;
l/S – характерное для ферритового кольца отношение среднего пути магнитного потока к площади сечения магнитного потока в его стенках.

 

Электродвижущая сила самоиндукции равна:

 

 

U =  – L*dI/dt

(6)

 

Т.е. ЭДС катушки будет препятствовать изменению величины электрического тока в ней. Будет тормозить электрон, влетающий в ферритовое кольцо и ускорять электрон, покидающий последнее. Отсюда изменение импульса электрона P(x) и относительной фазы волновой функции df, как записано в формулах (1) и (2).

На Фото.2 показана электрическая катушка 3, ток в которой создает в ферритовом кольце свое магнитное поле, задает свой магнитный векторный потенциал внутри ферритового кольца. Который можно определить по интегралу по всему окружающему объему пространства:

 

 

 

 

 

(7)

 

Где J – электрические токи на расстоянии r от точки наблюдения.

 

Но физически проще представить, что энергия запасенная в ферритовом кольце (см. Фото.2) в виде магнитного поля равна:

 

 

W ≈ µ0*µ*(Hk ± He)2 = µ0*µ*(Hk2 ± 2*Hk*He + He2)

(8)

 

где

Hk – магнитное поле катушки 3 создаваемое в ферритовом кольце 2;
He – магнитное поле проводника тока 1 (движением электрона) создаваемое в ферритовом кольце 2.

 

Добавка энергии  ± 2*Hk*He обуславливает изменение импульса электрона P(x) и относительной фазы волновой функции df, как записано в формулах (1) и (2).

 

Стоит отметить, что магнитная проницаемость вакуума µ0 характерна ко всему пространству, а не только для ферритового кольца. Т.е. можно представить, что для электрона постоянно существует некая индуктивность пространства L0 что проявляется как появление инерционной массы у электрона.

Кинетическая энергия электрона:


 

W = (me * v2)/ 2 ≈ L0*I2 / 2= (L0 * q2*v2/re2) / 2

(9)

 

где

me – масса электрона;
v – кинетическая скорость электрона;
I – электрический ток обусловленный движением электрона;
q – электрический заряд электрона;
re – «размер» электрона.

 

 

Тематическое содержание

СОДЕРЖАНИЕ