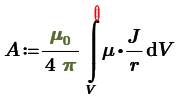Alexandr
A.Shpilman ( alexandrshpilman78@gmail.com )
Physics and/or mathematics
Nowadays,
“physicists” have deified mathematics so much that physics itself has been lost
in articles and textbooks. For example, let's take something from quantum
mechanics. So the change in the momentum of an
electron P(x) when moving in electromagnetic fields is written as
follows:
|
|
P(x)=P0-SQRT(q*U(x)*m)–
q *A(x)/c |
(1) |
|
where |
P0 – initial electron momentum; |
Changing
the relative phase of the wave function:
|
|
df~P(x)*dx= (P0-SQRT(q*U(x)*m)– q*A(x)/c)*dx |
(2) |
If
changes in the electron momentum in electric fields are obvious, then what does
the magnetic vector potential A have to do with it? It is believed that
magnetic induction:
|
|
B = rot A |
(3) |
And electric field intensity:
|
|
E = - dA/dt |
(4) |
What's the point of such a thing as magnetic vector potential A ?
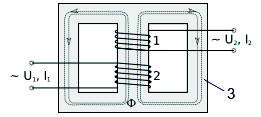
For example, consider a conventional electrical transformer in
Fig.1
|
|
|
Fig.1 |
Where 1 and 2 are the primary and secondary electrical windings. 3 –
ferromagnetic core of the transformer.
The entire magnetic field is concentrated in the ferromagnetic core of
the transformer. Its effect on electrical windings is minimal. The main factor
operating the electric windings 1 and 2 is the magnetic vector potential A.
And the electric induction field is determined by formula (4).
Before returning to formulas (1) and (2), consider Photo.1 and Photo.2,
where 1 is an electrical conductor, 2 is a ferrite ring, 3 is an electrical
winding on a ferrite ring.
|
|
|
|
Photo.1 |
Photo.2 |
The inductance of the electrical “coils” in Photo.1 and Photo.2 is equal
to:
|
|
L ≈ µ0*µ*N2/(l/S) |
(5) |
|
where |
µ0
– magnetic permeability of vacuum; |
The electromotive force of self-induction is equal to:
|
|
U = – L*dI/dt |
(6) |
Those, the EMF of the coil will prevent the magnitude of the electric
current in it from changing. It will slow down the electron flying into the
ferrite ring and accelerate the electron leaving the latter. Hence the change
in the electron momentum P(x) and the relative phase of the wave
function df, as written in formulas (1) and (2).
Photo.2 shows an electric coil 3, the current in which creates its own
magnetic field in the ferrite ring and sets its magnetic vector potential
inside the ferrite ring. Which can be determined by the integral over the
entire surrounding volume of space:
|
|
|
(7) |
Where J are
electric currents at a distance r from the observation point.
But physically it is easier to imagine that the energy stored in a
ferrite ring (see Photo.2) in the form of a magnetic field is equal to:
|
|
W ≈ µ0*µ*(Hk ± He)2
= µ0*µ*(Hk2 ± 2*Hk*He + He2) |
(8) |
|
where |
Hk – magnetic field of coil 3
created in ferrite ring 2; |
Äîáàâêà ýíåðãèè ± 2*Hk*He îáóñëàâëèâàåò èçìåíåíèå èìïóëüñà ýëåêòðîíà P(x) è îòíîñèòåëüíîé ôàçû âîëíîâîé ôóíêöèè df, êàê çàïèñàíî â ôîðìóëàõ (1) è (2).
The addition of energy ± 2*Hk*He causes a change in the electron momentum P(x)
and the relative phase of the wave function df, as written in formulas
(1) and (2).
It
should be noted that the magnetic permeability of
vacuum µ0 is characteristic of the entire
space, and not just of the ferrite ring. Those. one can imagine that for an
electron there is always a certain inductance of space L0,
which manifests itself as the appearance of an inertial mass in the electron.
Electron
kinetic energy:
|
|
W = (me
* v2)/ 2 ≈ L0*I2 / 2= (L0 *
q2*v2/re2) / 2 |
(9) |
|
where |
me
– electron mass; |