Alexandr A.Shpilman ( alexandrshpilman78@gmail.com )

Russian

Coherent an Electrical Current

Fig.1

Fig.2

Fig.3

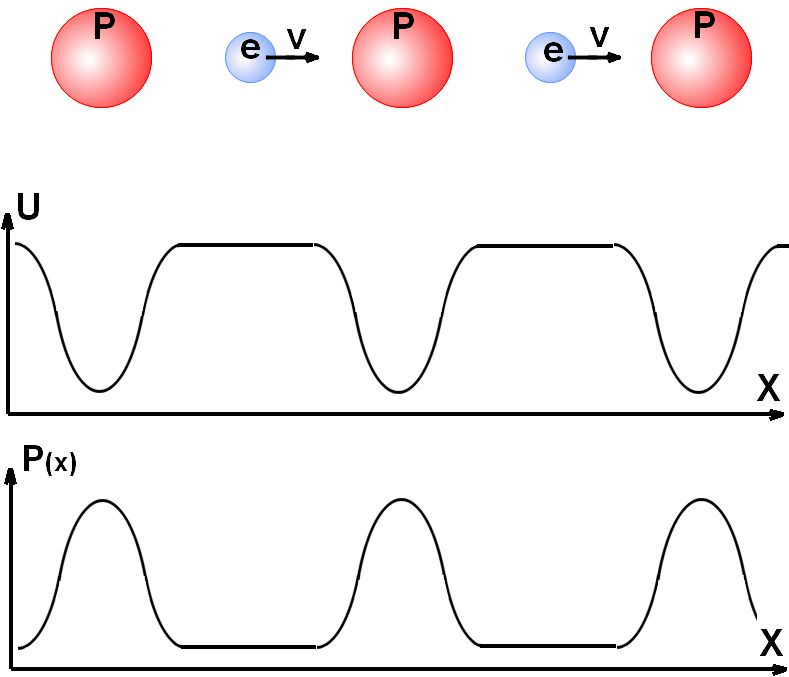
At a motion of the electrons e (see Fig.1) in a conductor along the coordinate x, the electrons move in a field of varied electrical potential U of the atoms’ lattice of the metal P.

Thus the impulse of the electron e is equal:

P(x)=P0-SQRT(q*U(x)*m)

where

P0 – is an initial impulse of an electron; q - is an electrical charge of an electron; m – is a mass of an electron; SQRT – is a square root.

Changing of a relative phase of a wave function:

df~P(x)*dx= (P0-SQRT(q*U(x)*m))*dx

I.e. the electrons will have different increase of a wave function’s phase at a motion on different trajectories in a crystalline lattice of metal. If we shall reduce an oscillations’ amplitude of an impulse of an electron P(x), we can reduce the straggling change a phase of a wave function of electrons and thus, probably, the achievement of a coherence of electrons’ motion is possible.

It is possible to manipulate by an effective impulse of an electron P(x) changing the vector potential A(x). Thus:

P(x)=P0-SQRT(q*U(x)*m)– q *A(x)/c

where

c – is a velocity of light.

The change of a relative phase of a wave function will be:

df~P(x)*dx= (P0-SQRT(q*U(x)*m)– q*A(x)/c)*dx

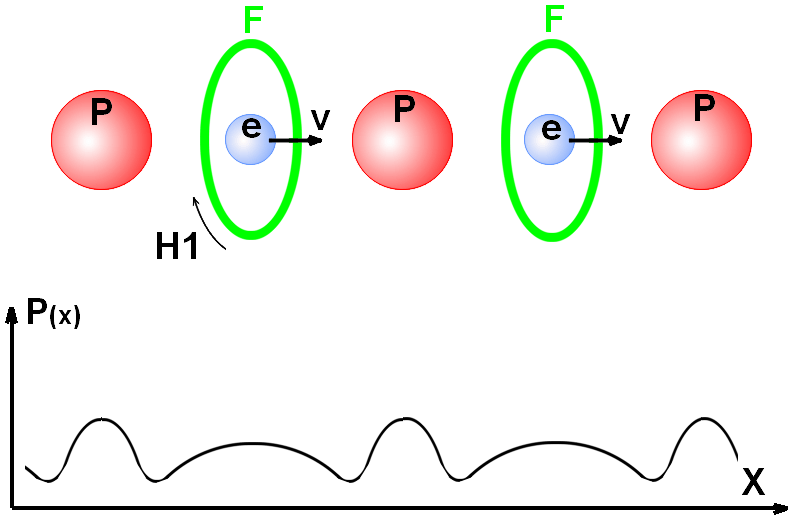
If we dispose ferromagnetic atoms between the atoms of an electrical conductor, these ferromagnetic atoms can strengthen the ring of magnetic field H1 of a moving electron. Vector potential A(x) of this ring of magnetic field will reduce the change of an effective impulse of an electron as it is shown in Fig.2.

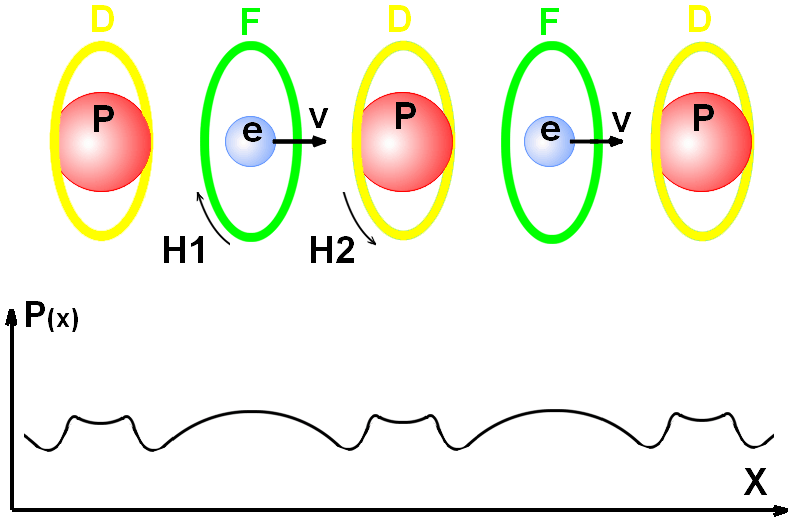
If we dispose diamagnetic atoms around the atoms of an electrical conductor, these diamagnetic atoms can attenuate a ring magnetic field of a moving electron. It is equivalent to occurrence of a magnetic field H2 directional opposite to the magnetic field H1. Vector potential A(x) of this ring of magnetic field will reduce the change of an effective impulse of an electron as it is shown in Fig.3.

In the result, the change of a relative phase of a wave function of electrons will be possible so small that the occurrence of a coherent current of electrons will be possible at high temperatures.

Probably, it is a model of a high-temperature superconductor, in which, for example, it is possible to use ferromagnetic atoms Fe, Co, Ni and diamagnetic atoms O, C, Bi.

Thematic Contents

CONTENTS