Alexandr A.Shpilman ( alexandrshpilman78@gmail.com )

Russian

How does electric current flow in a conductor?

It is well known, but not advertised, that a direct electric current in a conductor does not flow in a continuous stream. If we try to show what it looks like in the cross section of conductor 1, we will have many “jets” 2 of current of electric charges in the conductor.

Why this is so, no explanation is given.

Let's consider a picture of the magnitude of the magnetic vector potential A (3) between two long, parallel electrical conductors 1 and 2 with an electric current flowing through them in one direction.

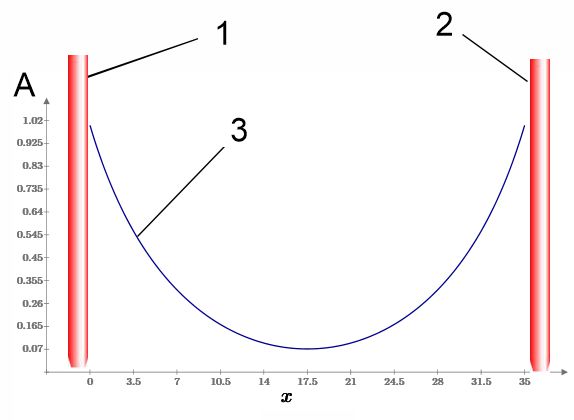
The magnitude of the magnetic vector potential 3 is equal to:

A(x) ~ j* (1+ln(a/(a+x)) + ln(b/(b-x)))

(1)

where

j – the magnitude of the electric current in the “jet” (b – a) – the distance between the surfaces of adjacent “jets”.

Formulas from quantum mechanics:

P(x)=P0-SQRT(q*U(x)*m)– q *A(x)

(2)

where

P0 – initial electron momentum; U – electric potential; A – magnetic vector potential; q - electric charge of an electron; m – electron mass; SQRT – Square root.

Change in the impulse of an electric charge carrier in a “jet” of electric current:

p(x) ~ – q*A(x)

(3)

Change in the speed of an electric charge carrier in a “jet” of electric current:

v(x) ~ – q*A(x)/m

(4)

Those. the speed of electric charges in the “jet” decreases. For electric charges moving in the vector potential, an electric field also appears:

E(x) ~ – grad(A(x))

(5)

Which will pull free electric charges in the conductor into the resulting “jets” of electric current. Until this field exceeds the electric field from an increase in the charge density in the “jet”.

It must be assumed that this kind of instability in the flow of electric current will manifest itself in both superconductors and electrolytes.

Но подобное возможно только в сверхпроводниках, но при этом уже начнут проявляться квантовые эффекты. В обычных проводниках ситуация другая. Вспомним закон Ома:

U = R * I

(6)

where

U – conductor voltage drop, R - electrical resistance, I - the magnitude of electric current in a conductor.

In our case, the following condition must be met:

jp/σ = Ei

(7)

where

jp – current density in the "jet", σ - local specific conductivity of an electric conductor, Ei - the electric field created in a conductor by a current source.

It is worth considering that here σ is precisely the local specific electrical conductivity of the electric current conductor, which will be greater than the value for the material of the electric conductor recorded in reference books. Since the latter is already integral over the full cross-section of the conductor, taking into account areas with minimal flow of electric current.

It is worth recalling that free electric charges in metals are not free in reality. See Foucault currents. So in reality the situation is more complex and the figures often given in articles for the speed of flow of electric charges in a conductor are incorrect.

Thematic Contents

CONTENTS